A mathematician, like a painter or a poet, is a maker of patterns… The mathematician’s patterns, like the painter’s or the poet’s must be beautiful; the ideas like the colours or the words, must fit together in a harmonious way. Beauty is the first test.
GH Hardy
As some readers will no doubt be aware, I’m no mathematician. It might then seem presumptuous to take a view on the teaching of numeracy, but I think the fact that I’m not naturally numerate gives me a perspective that other, more mathematically minded thinkers might lack.
My first, rather trite observation is that numeracy is not the same as literacy. Being literate – able to read, write and communicate – is, to one degree or another, essential for all school subjects. Despite the clunky misnomer, ‘literacy’ (and by literacy I mean language) is present in every lesson whether we want it there or not. Unless you’ve perfected some innovated new mime method of teaching (and if you have I’d like to hear – or even better, watch – your explanation) teaching by its very nature depends on language to convey ideas to pupils. Numeracy, on the other hand, is not a universal constant across all lessons.
But, like literacy, the concept of ‘numeracy’ desperately needs some unpicking. What, for instance, is the difference between numeracy and maths? Numeracy is just one component of mathematics and not, perhaps, the most important. Numeracy, being numerate, is the ability to understand and work with numbers. Working with numbers is important, essential even, but irrelevant in various subjects. Much better, I think, to talk about ‘mathematical thinking’ than numeracy. Mathematical thinking encompasses something so much broader and arguably is relevant to all curriculum areas.
Just as there are many atrocities committed in the name of literacy, at its worst numeracy across the curriculum is a concept so superficial it’s barely even there. I’m not saying it’s actually harmful, but what’s the point of this?
I get the point that we can find mathematics in everything, but is this kind of generic numeracy activity really a useful way to start lessons?
Here are a few other examples I’ve seen perpetrated by real teachers in real schools:
- English: count the number of lines in a poem
- Art: calculate the amount of paint needed to cover your canvas
- History: Multiply the number of King Henrys by the number of King Georges
- PE: time yourself running 100m, take your pulse, draw a graph…
For pity’s sake, why? These activities just waste valuable curriculum time and accomplish little beyond irritating students. But I understand why we do this – maths has an image problem. The fact that many children perceive maths as boring and irrelevant is endemic and needs addressing. It’s important for all teachers to unite against the idea that being bad at maths is socially acceptable. It isn’t. So I really get the misguided urge to make teachers cheerfully shoehorn numbers where they don’t really belong.
As an alternative however, there might be real worth in the concept of ‘thinking like a mathematician’, but what exactly does this entail? As far as I can work out, there are, broadly, four areas of maths:
- Number
- Operations & calculations
- Shape, space & measures
- Data handling
The first two have very limited applications across the curriculum but the second two are, potentially useful everywhere.
These are some of the ways mathematical thinking might naturally occur across the curriculum:
- Identifying structures & relevant data
- Being systematic
- Searching for patterns
- Thinking logically
- Predicting & checking
- Breaking down problems into smaller parts
- Interpreting solutions in context of problem
- Estimating to check likelihood of answers
These ways of holding the world are not only essential for an understanding of mathematics but also enrich every area of life. As such, it might pay us to make these things explicit.
So, what could we do in lessons?
Here are some possibilities:
1. Sequencing
In order to help students think systematically, logically and to break down problems into smaller parts it helps to see things sequentially. Six Degrees of Separation (or The Kevin Bacon Game as it’s sometimes known), is useful way to get pupils to reflect on the explanations we’ve offered. If you’ve never encountered this before, it’s based on the theory that every human being in the world is connected to every other human being through a chain of no more than six people. The idea is that they need to logically sequence their understanding from one concept to another. We could provide pupils with a prompt connected to the topic we’re studying, give them an end point they have to connect to and get them to sequence what they know:
- Select a topic or theme.
- Write 1–6 along a timeline.
- Put your topic at number 6.
- Get from the stimulus to your topic in no more or less than six steps.
So we might ask them to suggest the six degrees of separation between the assassination of Archduke Ferdinand and the outbreak of the Great War, or between Pip’s first meeting with Magwitch and his discovery that he has ‘great expectations’. To keep them on track, we might specify that step 4 must be the introduction of Mr Jaggers, or the Ottoman-German Alliance or whatever. And if six degrees is too few or too many then feel free to extend the chain as far as you think it should stretch.
2. Asking mathematical questions
In most subjects there are times when we want students to consider what they’re learning about in a mathematical way. It might therefore be useful to ask them to frame question about curriculum content in mathematical terms:
- How could you sort these…….?
- How many ways can you find to ……. ?
- What happens when we ……… ?
- How many different ……. can be found?
- What is the same/different?
- Can you group these ……. in some way?
- Is there a pattern?
- How can this pattern help you find an answer?
- What do think comes next? Why?
- Is there a way to record what you’ve found that might help us see more patterns?
- What would happen if….?
3. Domain specific thinking (with maths)
And asking these kinds of questions could help prompt student to think about subject content using the tools of mathematics:
- specialising – trying special cases, looking at examples
- generalising – looking for patterns and relationships
- conjecturing – predicting relationships and results
- convincing – finding and communicating reasons why something is true.
4. Organising information
The Venn Diagram useful way to organise and present information across a
range of subjects.
One drawback though is that the overlapping space can be too cramped to contain much writing. An alternative is to use Comparison Alley where information is organised in such a way that there’s plenty of space to make the comparison:
5. Presenting information
Maths provides new and useful ways of seeing the world. Many if not most subject areas can find space to expand students’ thinking by asking them to express their understanding using the tools of mathematics. For instance I have on various occasions used each of the following in English lessons:
- Graphs
- Timelines
- Flow charts
- Graphic organisers
- Pie charts
Here’s some examples from different subjects:
6. Seeing relationships
Size matters. Understanding how big something is in relation to something else can be important in all sorts of lessons. Another area where we might benefit from mathematical thinking is scale. A favourite example is how we can get students to wrap the head around how big a billion is:
- A million seconds = 11 ½ days
- A billion seconds = 32 years
Or maybe these examples could be useful:
It’s also important to see the mistakes we make when we try to establish patterns.
7. Accuracy matters
Maths also has something to teach us about attention to detail, particularly the difference between ‘getting it right’ and ‘getting it done’. Where can we apply the concept of ERROR CHECKING across the curriculum?
- Dates in history?
- Notation in music?
- Learning lines in drama?
- Punctuation in English?
So, in summary, the secret of numeracy is that it’s not really (or not just) about numbers. Being unable to use numbers is of course severely limiting but being unable to think mathematically is socially unacceptable. We use mathematical thinking all the time, the trick is to make it explicit to students. If you explain how your subject uses maths to organise and express ideas, then maybe prejudices will slowly start to shift.
My best thinking on whether to include an activity in your lesson in the name of numeracy is to ask if it helps students think about the subject content you’re teaching. If it doesn’t, it’s a waste of time.



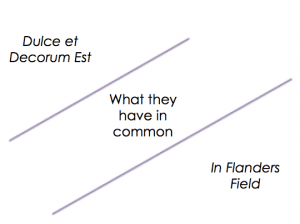








As a maths teacher, I love this!
not only does it show that maths isn’t all about the numbers (something I think even math teachers miss sometimes), but also highlights what maths is about and how you use it almost without knowing .
A great read.
Thank you Alex – good to hear.
David, I would recommend you reading “A Mathematician’s Lament” by Paul Lockhart for another view on what Mathematics is and could be in schools – it’s a real Jerry Maguire moment. You can find his original 22 page paper online and the book is just a little longer. Agree or not with him, it is a great and interesting read. I gave copies to all my colleagues i the maths department and it was like watching a firework go off.
Hi Thom – I have read the mathematician’s lament. Didn’t really buy it though. Have you read this? http://www.ccs.neu.edu/home/matthias/Tmp/essays/essays/anti-lament.html
Love this post – I really like the ‘six degrees of separation’ activity. To push it one step further this could well be cross curricular – link trigonometry to the War of Roses. Or they could link any current topic in Maths (I mostly teach Maths) to any current topic in any other subject. I will definitely be doing this. Well done, David. Love the blog.
[…] along comes David Didau with his The Secret of Literacy, and a number-bomb explodes. @Mr_Numerator gets the Numeracy across the Curriculum job and suddenly […]
Love this posts! A great read!
[…] The Secret of Numeracy. Street Math | Laura Overdeck | TEDxJerseyCity. […]
Thanks for this, I was just about to send everyone a long list of “things that are numeracy” So we could develop our numeracy strategy. It looked like a long list. Boxes would be ticked. Move on.
This is a much more powerful approach and will make us think more deeply.
Hi David
I am in the process of putting together a resource for our school to help teachers find ways to teach numeracy across the curriculum, and as part of my research I found this link. Where have you been all my teaching life???? This has got to be one of the most useful pieces of writing I have found on numeracy across the curriculum. It’s witty and provides the “how” not just the “what”. We are all experts on “what is wrong” but not many are able to provide the “how” that is real and not just fluff!
I have become a little tired of the negativity non-Maths teachers have towards numeracy, and from a numeracy perspective you have summed up everything we do in the classroom so well. We don’t think of sequencing activities as mathematical but they are – it’s patterns and patterns make up a large portion of what we teach students from kindergarten! I thought I was pretty knowledgeable when it came to teaching numeracy but I have to say that after reading your article I realised that I still had so much to learn. Thank you!
I need you to know that I will be including this link and a summary of what you have presented here in our resource and urging teachers to visit this link.
Best wishes
Hadla
Thanks Hadla, glad to be of help.
At last, someone is talking sense about numeracy!
Wow. Possibly the best summing up of numeracy in the curriculum I’ve read. Top work that man.
[…] The Secret of Numeracy (across the curriculum) A mathematician, like a painter or a poet, is a maker of patterns… The mathematician’s patterns, like the painter’s or the poet’s must be beautiful; the ideas like the colours or the words, must fit together in a harmonious way. Beauty is the first test.GH Hardy As some readers will no doubt be aware, I’m no mathematician. […]